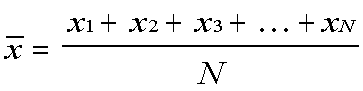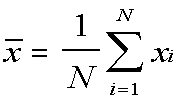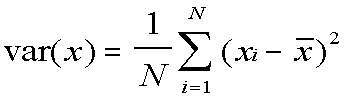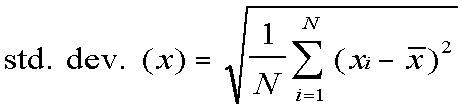University of South Carolina, Arnold School of Public Health, Dept. of Health Services Policy and Management, HSPM J716

Introductory Probability and Statistics Review

This page goes over some basic probability and statistics concepts that you got in BIOS 700.

Probability

The probability of an event is a fraction between 0 and 1.

1 is the probability of an event that is sure to happen. The probability that the sun will rise tomorrow is 1.

0 is the probability of an event that cannot happen. The probability that a Bridge hand will contain a Joker is 0, because Bridge is played with a deck from which the Jokers have been removed.

Here's how you get probabilities between 0 and 1: Suppose there are a number of equally likely events. Some events represent a "win" and some a "loss." The probability of winning is the number of winning events divided by the total number of events. Such well-defined situations arise in practice only in games.

For example, consider a coin with a "heads" side and a "tails" side. If we assume that the two sides are equally likely to be up when the coin is tossed and lands on a table, then the probability of "heads" is 1/2 and the probability of "tails" is 1/2.

For another example, an American roulette wheel has 38 spaces. Each space has a number and a color. Eighteen of the spaces are red. Eighteen are black. Two are green. If you bet that the ball will fall in a red space, your probability of winning is 18/38.

Your turn:
A deck of playing cards has 52 different cards, if we remove the Jokers. I draw a card at random from that deck. What is the probability that the card will be the Queen of Diamonds?

For your answer, you can type two numbers with a slash / sign in between to indicate division. Alternatively, you can type in a decimal number.
Enable Java on your computer to use this applet.

The Law of Large Numbers

If a trial (such a play of a game of chance) is repeated many times, then the more times the trial is repeated, the more likely it is that the frequency of any particular event will be close to the probability of that event. For example, if we flip our coin many times, the more times we flip it, the more likely it is that the the number of "heads" divided by the total number of tosses will be close to 1/2. This may be taken as the definition of probability, or it can be taken as a theorem, in which case it is called the Law of Large Numbers.

Law of Large Numbers Example

This applet simulates tossing a coin over and over again. Click Start to start the coin tosses. This same button restarts the tosses if you stop them with the Stop button. Click Faster to reduce the delay time between simulated tosses.
Enable Java on your computer to use this applet.
This coin, simulated by a random number generator, has two sides that are equally likely to come up. If you let this run, the proportion of heads in the number of tosses will approach one-half (0.5). Rarely will the proportion be exactly 1/2. Instead, it will fluctuate around 0.5, with the fluctuations slowly getting smaller.

Statistics

A statistic is a number calculated from numerical data. An example of a statistic is the mean.

Mean

The mean of a list of numbers is calculated by adding all the numbers up, then dividing by how many numbers there are. The mean is also called the "average."

Some examples:

Your turn:

What is the mean of these numbers: 1, 1, 2, 8?
Enable Java on your computer to use this applet.

The mean is a measure of central tendency. The mean height of 21-year-old men in the U.S. is 177 cm, or 5' 10". The mean height of women here is 164 cm, or 5' 4". This tells us that, in the U.S., men are generally taller than women. It does not imply that every man is taller than every woman.

Expected Value

Suppose have a game of chance with a numerical outcome. For example, we can flip our coin painted with "0" and "1" and see which number comes up. The expected value is calculated by taking each outcome and multiplying its value by the probability of that outcome, then adding all the products up.

For the coin, the expected value is:
(0 times the probability of 0) + (1 times the probability of 1).
If the coin is fair, so that the two sides are equally likely to come up, then the expected value is:
(0 times 1/2) + (1 times 1/2) = 0 + 1/2 = 1/2.

If all outcomes are equally likely, then the expected value will equal the mean of all the outcomes.

Suppose we flip our coin many times, and calculate the mean of all the outcomes of the tosses. The more flips we do, the more likely it is that the mean of all the accumulated outcomes will be close to the expected value. The simulation above does this. If you say that a head is worth 1 and a tail is worth 0, the "proportion of heads" fraction is the mean of all the outcomes so far. It does tend to get closer and closer to 0.5.

Variance

The variance measures how spread out a list of numbers is, how much the numbers differ from their mean. To calculate the variance:
 
General instructions 
for calculating a variance:		 For example, suppose you have
a coin with 0 and 1 painted on its sides:
Take each data item. The data items are 0 and 1.
Subtract the mean from each. Subtract the mean ( 1/2 ) from each: -1/2 and 1/2
Square each. Square each: 1/4 and 1/4 
Add them all up Add them all up: 1/4 + 1/4 = 1/2
Divide by the number of data items
to get the variance.		 Divide 1/2 by the number of data items ( 2 ), to get 1/4.
The variance is 1/4.

Your turn:

What is the variance of these numbers: 3, 3, 3, 3. (Yes, the four numbers are the same.)
Enable Java on your computer to use this applet.

This one is harder:
What is the variance of 1, 1, 2, 8?
Enable Java on your computer to use this applet.

Notice that 3, 3, 3, 3 and 1, 1, 2, 8 have the same mean but different variances. If you were designing a system for handling eggs, you would want to know the both mean and the variance of the size of the eggs.

Standard Deviation

The standard deviation is the square root of the variance. Like the variance, the standard deviation measures spread. The variance involves squaring the data numbers. Taking the square root of the variance gives you a number that is in the same units as the original data. This allows for an intuitive interpretation of the standard deviation: Usually, depending on the shape of the distribution (see next), about 2/3 of the data numbers are within one standard deviation of the mean.

Distributions

If the outcome numbers are discreet, meaning that there is a certain number of possible outcomes, then the distribution is a list of all possible outcomes and each one's probability.

If the outcome numbers are continuous, meaning that the outcome could be any number in either a finite range or an infinite range, then you can't list all possible outcomes and each one's probability. What you can do instead is give a mathematical formula that would tell you, for any given x , what the probability is that the outcome will be less than x . This is the distribution function. Distributions are often visualized using the density function. On a graph of the density function, if you pick any two possible outcome values on the x axis, and draw vertical lines at those values up from the x axis to where they intersect the density function's curve, then you will have an enclosed area with straight sides, a straight botton, and a curved top. The size of that area tells you the probability that the outcome will be between the two x values.

For example, a distribution we'll be using often this semester is the normal distrbution. Its density function is "the bell curve."

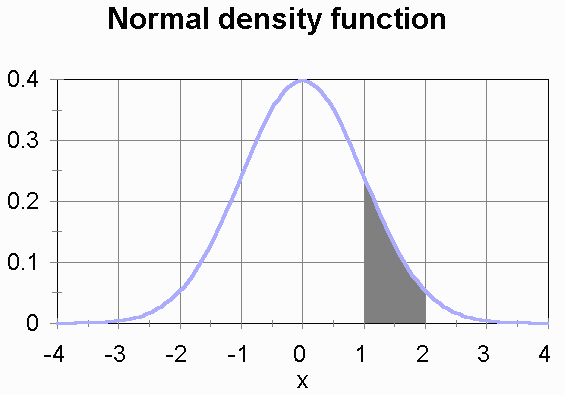
This is the density function for a normal distribution with a mean of 0 and a standard deviation of 1. The density function is constructed so that the total area under the curve is 1. (The area under the curve is unbounded, because the curve goes off forever in both directions without ever quite touching the x axis, but even so the area under the curve is finite and equal to 1.) The area of the shaded region is the probability of a outcome number between 1 and 2.

Algebraic Expressions with Summation Signs

For these expressions, the data items are represented as:

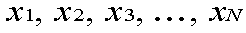
There are N data items.
For our coin with a 0 on one side and a 1 on the other, the data items are x1 = 0 and x2 = 1. N = 2.

Mean

The mean is represented by x with a line over it, read "x bar."

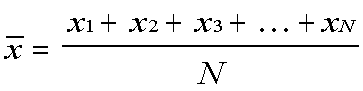
A shorter notation for this uses the summation sign, the capital sigma:

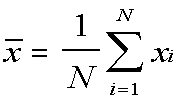
This means:
  1. Substitute 1 for the i in the expression to the right of the big sigma. This gives you the first data item.
  2. Keep substitutimg successive numbers for i until you have substituted N for i. This gives you the second through the Nth data item.
  3. Add all those terms up.
  4. Divide the sum by N.
This is read, "X-bar equals one over N times the sum, from i equals 1 to N, of x-sub-i."

The course readings use this notation often. If it seems intimidating, take the time to work through what the expression means. Proceed methodically and you can do it.

Variance

The variance is:

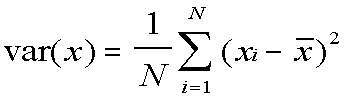
You can read a formula like this from the inside out:
  1. Take a data item (xi).
  2. Subtract the mean from it ( - x-bar).
  3. Square the difference (the 2 exponent outside the parentheses).
  4. Do the same for the 1st through the Nth data item (the i=1 below the Sigma and the N above it).
  5. Add them all up (what the Sigma means).
  6. Divide the sum by the number of data items (the 1/N in front).

Standard Deviation

The standard deviation is the square root of the variance.

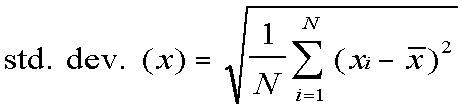
The views and opinions expressed in this page are strictly those of the page author. The contents of this page have not been reviewed or approved by the University of South Carolina.
E-mail: