Economics Interactive Lecture (Instructions)

The Internal Rate of Return

Copyright © 1997-2006 Samuel L. Baker

When you are evaluating an investment, a useful number number to know is the internal rate of return.

For some investments, like bank accounts, the internal rate of return is easy to figure because the bank tells you what it is. For example, a 5% simple interest bank account has an internal rate of return of 5%.

For other investments, you have to do some work to calculate the internal rate of return. This is especially true of investments like building a factory or getting an education. These kinds of investments generally don't pay money in nice even amounts like a bank account does. Nevertheless, you can calculate an internal rate of return for these investments, and use it to decide which investments pay best.

To evaluate investments and calculate an internal rate of return, we need the concept of income stream.

Income Stream

In the grubby world of economic theory, where money is everything, any investment can be expressed as an income stream. An income stream lists years (or months or whatever) and the amounts of money that flow in or

An Income Stream Example

Here is the income stream for what you get if you

  1. Put $1000 in a 5% simple interest bank account
  2. Take out the $50 interest each year. ($50 is 5% of $1000.)
  3. Take all the money out at the end of the sixth year.
Year 0 1 2 3 4 5 6
Income -$1000 $50 $50 $50 $50 $50 $1050
In Year 0, which represents Now, we put $1000 in the bank. We put a negative number, -$1000 in for Income in Year 0, because the $1000 flows out from us.
Year 0 1 2 3 4 5 6
Income -$1000 $50 $50 $50 $50 $50 $1050
In years 1 through 5, we will get paid $50, 5% of $1000. The 50's above are positive numbers, showing that the money flows to us.

Note: To keep things simple, we imagine that interest is paid annually. Most real life bank accounts pay interest monthly. Also, we imagine that we withdraw each year's interest payment from the bank. We don't leave it in the bank to compound (earn interest on the accumulated interest) during the following years.
Year 0 1 2 3 4 5 6
Income -$1000 $50 $50 $50 $50 $50 $1050
Imagine that at the end of year 6 we take our $1000 back. Our total income in year 6 is $1050, the $1000 principal plus the $50 interest we get in year 6.

An Alternative Investment

Now let's consider an investment that our financial vice president has proposed as an alternative to putting our $1000 in the bank for six years. This investment involves buying a machine that will cost $1000. It will give us $200 in operating profit per year for six years, starting the year after we buy it. At the end of six years, the machine will have no value, due to wear and obsolescence. There's no lump of money waiting for us at the end, as there is with the bank account.

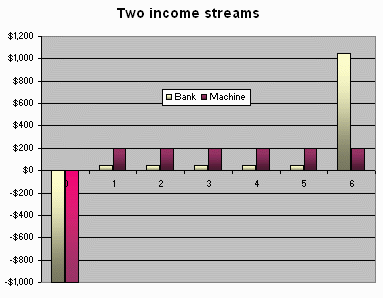
This table shows the bank income stream and the machine income stream.
Year 0 1 2 3 4 5 6
Bank -$1000 $50 $50 $50 $50 $50 $1050
Machine -$1000 $200 $200 $200 $200 $200 $200
It's not obvious which investment is better, is it? We could try adding up the income streams ...

Bank Account: -1000 + 50 + 50 + 50 + 50 + 50 +1050 = 300

Machine: -1000 +200 +200 +200 +200 +200 + 200 = 200

The income stream from the bank account adds up to $300. The income stream from the machine adds up to $200. Does this make the bank account better?

The key is "present value" concept.  This concept is reviewed below, but it is introduced in its own Interactive Tutorial on Discounting Future Income. Please try that tutorial now if the above question puzzled you.

The point is:  The bank account income stream pays more money in total, but most of that income is in the big lump of $1050 in year 6. The machine pays less in total, but it pays more money per year in the years that come sooner.  Getting the money sooner is what may make the machine's income stream have a higher present value than the bank's.

The Present Value of an Income Stream

The present value of a future amount of income is:
Present Value = (Future Value)/(1 + Discount Rate)ª,
where the exponent ª is the number of years in the future that the future value will be received. The discount rate is the same as the interest rate.

An income stream is a series of future values. The present value of an income stream is calculated by adding up the present values of all the items in the income stream.

To calculate a present value, we need to pick a discount rate. Since one of our alternative investments is a 5% per year bank account, let's pick 5% per year as the discount rate.
Year (a in the formula below) 0 1 2 3 4 5 6 Total
Machine income stream -$1000 $200 $200 $200 $200 $200 $200
1.05ª 1.0000 1.0500 1.1025 1.1576 1.2155 1.2763 1.3401
Present values, at a 5% discount rate -$1000 $190.48 $181.41 $172.77 $164.54 $156.71 $149.24 $15.14
Each of the numbers in the Present values row is the number above it in the Machine income stream row, divided by 1.05ª, where the exponent ª is the year number.

The total of these present values is $15.14. This is the present value of the machine income stream at a 5% discount rate. (If you check the addition, using the numbers shown in the table, you'll get $15.15, due to round-off error.) The tutorial on discounting future income has a nifty spreadsheet setup for calculating present values that you can copy and use in your own spreadsheet.

The fact that this $15.14 total is bigger than $0 is enough to tell us that the machine is a better-paying investment than a 5% interest bank account.

Not convinced yet? Let's find the total present value of the 5% interest bank account.
Year 0 1 2 3 4 5 6 Total
5% account income stream -$1000 $50 $50 $50 $50 $50 $1050
Present value, 5% discount rate -$1000 $47.62 $45.35 $43.19 $41.14 $39.18 $783.53 $0.00

These present values add up to $0. (Actually, they add to $0.01, but that's due to round-off error.)

The present value of an X% bank account, evaluated at an X% discount rate, will always turn out to be $0, no matter what X is.

At a 5% discount rate, the machine has a higher present value ($15.14) than the 5% bank account (with its present value of $0), so the machine is the better-paying investment.

The primitive method of adding up the income streams ...

Bank Account: -1000 + 50 + 50 + 50 + 50 + 50 +1050 = 300

Machine: -1000 +200 +200 +200 +200 +200 + 200 = 200

... would be valid if the interest rate were 0%. That would be if you could borrow money and pay it back without any extra for interest.

So far, so good, but what if we have other alternative investments? How do we compare them? How do we decide what discount rate to use?

Calculating the Internal Rate of Return

One way to compare investments is to calculate an internal rate of return for each one. The calculation we just made for the bank account gives us an idea of what we want to do. The bank account's interest rate (5%) was the discount rate that made the present value of its income stream total zero.

We can define the machine's internal rate of return the same way. The internal rate of return for the machine is the discount rate that makes the present value of the machine's income stream total to zero.

Consider this table:
Year 0 1 2 3 4 5 6 Total
Income stream -$1000 $200 $200 $200 $200 $200 $200
Present value, at a 5% discount rate -$1000 $190.48 $181.41 $172.77 $164.54 $156.71 $149.24 $15.14
Present value, at a 6% discount rate -$1000 $188.68 $178.00 $167.92 $158.42 $149.45 $140.99 -$16.54
At a 6% per year discount rate, the machine investment's present value is less than $0. At a 5% discount rate, the present value is greater than $0. The Intermediate Value Theorem implies that there is a discount rate between 5% and 6% at which the present value is $0. Let's find that discount rate.

The applet below allows you to change the discount rate to anything between 5% and 6%.  Use the slider on the left side. When the slider is all the way to the left, the discount rate is 5%. When the slider is all the way right, the discount rate is 6%. To move the slider, you can:

As you change the discount rate, the applet will recalculate the present value of the income stream.

Play with this a little. Move the slider right and left. See how this changes the present values of the future income amounts. Then fine-tune the discount rate to get the total present value as close as you can to $0. You won't be able to hit $0 exactly. When you have gotten the present value as close to $0 as you can, scroll down to see if your result is the same as mine.

Please do not scroll down past this area until you have tried the applet above.
The text
resumes
here:

Year 0 1 2 3 4 5 6 Total
Income stream -$1000 $200 $200 $200 $200 $200 $200
Present value, at a 5.47% discount rate -$1000 $189.63 $179.79 $170.74 $161.63 $153.24 $145.30 $0.06
A discount rate of 5.47% makes the total present value $0.06, which is as close as you can get to zero without going to the next decimal place. Thus, 5.47% is our best approximation the internal rate of return for the machine investment.

The machine investment's 5.47% internal rate of return is higher than the bank account's 5% rate of return. This is sufficient to tell us that the machine is a better-paying investment.

Two cautionary notes:

  1. The idea that better investments have higher internal rates of return is appropriate for comparing investments that have their costs first and their positive incomes later, and which have about the same initial costs. Our imaginary bank account and machine fit this criterion, so we are OK to use the internal rate of return for comparison. More on this issue at the end of this tutorial.
  2. Risk can complicate the comparison of investments. For this tutorial let us assume that the risks of our alternative investments are the same. In particular, we will assume that the machine is just as safe as the bank account.

    3. In real life, investments that offer better payback generally carry greater risks that the future income won't be paid. If the machine is riskier than the bank account, you may prefer the bank account, even if its internal rate of return is lower. Even so, the internal rate of return is useful to know. It tells you how much caution would cost you, or how much reward there is if you choose to assume some risk.
Let's look at the two investments again.  Here are the income streams and each investment's internal rate of return (IRR):
Year 0 1 2 3 4 5 6 IRR
Machine -$1000 $200 $200 $200 $200 $200 $200 5.47%
5% bank account -$1000 $50 $50 $50 $50 $50 $1050 5.00%
A student once asked: Suppose you don't need any money until year 6? Doesn't that make the bank account better? The total of the income stream (not discounted) is higher for the bank, and it gives you the money when you need it.

The answer is: Even if the times when you'll need money don't match when the investment pays, you should still go by the internal rate of return. That's especially true if the investment pays you money before you need it.

That's because you can use the bank, even if you buy the machine. You can deposit the extra income from the machine into a 5% account. At the end of Year 6, you'll have a bigger lump of money than you would have had if you had put your $1000 in the bank.

Here's how it works, in laborious detail, after you buy the machine in year 0 for $1000:

At the end of Year 1, you get $200. You keep $50 for spending, just like you would do for the bank account (according to what we assumed). You have $150 left over. You put the extra $150 into the bank. End of year 1:
Starting bank balance is $0.00. 
The machine pays you $200.00. 
You take $50.00. 
You add to bank account $150.00. 
Bank balance is $150.00. 
At the end of Year 2, the bank pays you 5% interest on your $150. That makes your bank balance $157.50. At the same time, you get another $200 from the machine. You keep $50 of that for spending, and put $150 in the bank. Your bank balance is $157.50 + $150 = $307.50. End of year 2:
Bank adds 5% of $150.00, which is $7.50. 
The machine pays you $200.00. 
You take $50.00. 
You add to bank account $150.00. 
Bank balance is $307.50. 
At the end of Year 3, the bank pays you 5% interest on your $307.50. That makes your bank balance $322.88. The machine pays you another $200. You keep $50 and put $150 in the bank. Your bank balance is $322.88 + $150 = $472.88.  End of year 3:
Bank adds 5% of $307.50, which is $15.38. 
The machine pays you $200.00. 
You take $50.00. 
You add to bank account $150.00. 
Bank balance is $472.88.
At the end of Year 4, the bank pays you 5% interest on your $472.88. That makes your bank balance $496.52. The machine pays you another $200. You keep $50 and put $150 in the bank. Your bank balance is $496.52 + $150 = $646.52.  End of year 4:
Bank adds 5% of $472.88, which is $23.64. 
The machine pays you $200.00. 
You take $50.00. 
You add to bank account $150.00. 
Bank balance is $646.52. 
At the end of Year 5, the bank pays you 5% interest on your $646.52. That makes your bank balance $678.84. The machine pays you another $200. You keep $50 and put $150 in the bank. Your bank balance is $678.84 + $150 = $828.84.  End of year 5:
Bank adds 5% of $646.52, which is $32.32. 
The machine pays you $200.00. 
You take $50.00. 
You add to bank account $150.00. 
Bank balance is $828.84. 
Finally, at the end of Year 6, the bank pays you 5% interest on your $828.84 That makes your bank balance $870.28. The machine pays you its last $200. Your withdraw the $870.28 from the bank, and you have $870.28 + $200 = $1070.28. By comparison, at the end of six years with the bank alone you get $1050. With the machine, you're ahead by $20.28. OK, it's not that much, but it does show that even if you don't need most of your money until Year 6, you wind up with more if you buy the machine. End of year 6:
Bank adds 5% of $828.84, which is $41.44. 
Bank balance is $870.28. 
The machine pays you $200.00. 
The total you finish with is $1070.28. 

Buy the machine, take out $50 a year from the proceeds, and you finish with $1070.28. Using the bank alone, you finish with $1050.

So, if you need $50 a year for five years, and then all the money after six years, the machine/bank combination is a better investment than the bank alone. You are better off buying the machine and then use the bank to earn interest on the money that you don't need right away each year.

If the machine investment pays you money after you need it (for instance, if you need $300 in Year 1) then you should compare the interest rate you'd pay to borrow money with the machine's internal rate of return.

A digression:  We keep talking about the "internal" rate of return.  Were you wondering if there is such a thing as an "external" rate of return?  There is, and the above analysis is an example, because it takes into account the interest that you can earn from machine's payments in the bank, which is an investment separate from, and thus "external" to, the machine investment itself. (Thanks to H.E.M. for putting me onto this.)
 

Internal Rate of Return Summary (so far)

The internal rate of return is the interest rate that makes the present value of the investment's income stream -- its costs and payoffs -- add up to 0.

The internal rate of return is a measure of the worth of an investment. If the risks are equal investments with higher internal rates of return pay better.
 
 

Some Applications

Let's look at three applications of the internal rate of return.

1. Evaluating a bond sold at a discount.

2. Detecting an economic shortage.

3. The effect of regulation on innovation.
 
 

Application 1. Evaluating a bond sold at a discount.

Here's a common type of investment, a bond sold at a discount.

The Sam's Software Corporation (a fictitious entity) is selling 5-year $1000 bonds that pay 10% interest per year. The bonds are selling at $900. How do you evaluate the bonds as an investment?

The first step is to figure out what the income stream is. Which of these is the income stream for a 5-year $1000 10% bond that's selling for $900?

Please do not scroll down past this area until you have tried the applet above.
The text
resumes
here:

Income stream for $1000 5-year bond, paying 10% interest, bought at $900.
Year 0 1 2 3 4 5
Income stream -$900 $100 $100 $100 $100 $1100
This is the income stream for the bond. The income stream goes 5 years into the future because it's a 5-year bond. The bond costs you $900 initially. It pays $100 (10% of $1000) in years 1-5. In year 5 it also pays its face value, $1000.

Since the nominal interest rate is 10%, let's evaluate the present value of this at 10%, and see what we get.
Year 0 1 2 3 4 5 Total
Income -$900 $100 $100 $100 $100 $1100
Income discounted at 10% -$900 $90.91 $82.64 $75.13 $68.30 $683.01 $100.00
The present value of this bond, evaluated at a 10% discount rate, is $100. Notice that this equals the amount of the initial price discount. That's because we discounted future income at the bond's stated interest rate. If the price of the bond had been $1000, instead of $900, then the present value evaluated at a 10% discount rate would have been $0, instead of $100.

Just to be sure we're all together here, please answer this:
The $683.01 number in the above table comes from the formula $683.01 = F/(1 + i)ª. Fill in the entry boxes below with the correct numbers for F, i, and a. (For each entry box, click in it to type in it, then press Enter to see if you're right. You can also use the Tab key to move from one box to the next.)

Let's find the internal rate of return for this bond. The applet below allows you to change the discount rate to anything between 0% and 20% by clicking and dragging the slide. To change the discount rate by 10%, click in the space between the slider and the end. To change the discount rate by 0.1%, click on the scrollbar's ends. As you change the discount rate, the applet will recalculate the present value of the income stream.

See how close you can get the total present value to $0. The discount rate at that the present value closest to $0 will be our approximation of the internal rate of return. As before, make a mental note of this discount rate, then go on.

Please do not scroll down past this area until you have tried the applet above.
The text
resumes
here:

Year 0 1 2 3 4 5 Total
Income stream -$900 $100 $100 $100 $100 $1100
Present value, 12.8% discount rate -$900 $88.65 $78.59 $69.67 $61.77 $602.35 $1.04
The discount rate that makes the total present value come closest to zero is 0.128 (12.8%), so the internal rate of return is 12.8%. This internal rate of return is the number to use to compare this investment with others. For bonds, the internal rate of return is also called the yield to maturity. It may be confusing, but the yield to maturity differs from the bond's nominal interest rate of 10%. That's because the bond is not selling for its face value.

Application 2: Detecting an Economic Shortage

Economists use the term economic shortage to mean a situation in which the quantity supplied of some good or service is less than what it would be if the market were functioning freely and competitively.

Shortages can manifest themselves two ways. One is with long lines of buyers or empty store shelves. The other is with prices higher than cost plus normal profit. (More on "normal profit" later.)

Detecting the first type of shortage is easy -- you just observe the lines or empty shelves. Detecting the second type is harder.

How do you judge when prices are high? Use the internal rate of return! We'll illustrate this with our machine investment example.

Suppose that there are two investments available to large numbers of investors. One is machines like this.
 
 

Our machine investment. But now, anybody can play.

Year 0 1 2 3 4 5 6 IRR
Income -$1000 $200 $200 $200 $200 $200 $200 5.47%
The other is the 5% bank account. The machine has a higher internal rate of return, at 5.47%, than the bank's 5%. What happens? Firms like yours take money out of the bank to buy machines.

As more and more firms buy machines, put them to work, and try to sell the machine's products, what would you expect to happen to the typical machine's income stream?

As the supply of the machine's products expands, and assuming that the demand curve stays the same, the prices of the machine's products should fall. This will cause the amount of income earned in years 2-6 to shrink. That will make the internal rate of return fall.

For example, suppose that annual income falls by just $1 to $199.
 
 

Here's the machine investment after competition starts to drive prices down:

Year 0 1 2 3 4 5 6 IRR
Income -$1000 $199 $199 $199 $199 $199 $199 5.31%
The internal rate of return falls to 5.31%, from the 5.47% it was before.

How far would you expect the income amounts to fall?

Please do not scroll down past this area until you have tried the applet.
The text
resumes
here:

Market equilibrium income for the machine under competition
Year 0 1 2 3 4 5 6 IRR
Income -$1000 $197.02 $197.02 $197.02 $197.02 $197.02 $197.02 5.00%
Once income falls this far, people will no longer want to take money out of the bank to buy machines. The supply of machine products will stop expanding, and the income you can get from a machine will stop falling. (Given the time lag in decision-making, income may fall further than this and then later come back up. Equilibrium will be reached when there's no incentive to shift money either from bank to machine or from machine to bank.)

How economic shortage fits with this:

If an investment has a high rate of return that persists over a long period of time, economists infer that competition must not be working as it should to lower income and equalize rates of return.

Normal profit is profit equivalent to what you could earn in the bank. No business would persist that didn't earn normal profit. Why put money into a business if you can do better in a no-effort bank account? But if the return to an investment stays higher than normal for a long time, that's an indication of an economic shortage, and some kind of monopoly restriction.

Some economists used to argue that the high rate of return to a physician's education showed that there was an economic shortage of physicians. In the late 1990s, managed care may reduce physicians' incomes to the point that there is an economic surplus, with below-normal returns, particularly to speciality training.

Application 3: Regulation Delays and the Internal Rate of Return

Changing the timing of future payoffs changes the internal rate of return.

Let's go back to our original machine investment again. Imagine that we have a patent to protect us against competitors and their price cuts.

Our machine investment, as before.

Year 0 1 2 3 4 5 6 IRR
Income -$1000 $200 $200 $200 $200 $200 $200 5.47%
Suppose, however, that meeting government safety regulations forces a delay in the start of sales of machine products. The income stream might change to this:
Machine with delayed income.
Year 0 1 2 3 4 5 6 7 IRR
Income -$1000 $0 $200 $200 $200 $200 $200 $200 ?????
The amounts in the income stream are the same, but the income is shifted forward by one year.

What happens to the internal rate of return?

Find the internal rate of return for this machine now. The applet lets you change the discount rate, starting from the old IRR of 5.47%. Move the slider to change the discount rate. Click to the side of the slider for a 0.01% change. See how close to $0 you can get the total present value.

Please do not scroll down past this area until you have tried the applet.
The text
resumes
here:

The discount rate that makes the total present value as close as you can get to $0 with this number of decimal places is 4.19%. The regulatory delay drops the internal rate of return to below what you can get from the bank. No one will invest in one of these machines now.

One way this machine's products could come to market would be if the prices for the machine's products go up. The prices would have to rise enough to make the internal rate of return as high as the bank's 5%. In this way, consumers wind up paying for the regulatory delay in higher prices. Notice that I didn't add any paperwork or testing cost to the calculations. The higher prices are purely because of the delay and the need to compete with other investments. Adding in the paperwork cost of complying with regulations would make the internal rate of return even lower.

Another way this machine's products could come to market would be if the price of the machine goes down. Like the discounted bond, a discount in the price of the machine would raise the internal rate of return. In this circumstance, the machine's manufacturer would pay the delay cost of the regulation.

Application 3. Does Regulation Discourage Research and Innovation?

The pharmaceutical industry argues that something much like this happened to them after 1962, when Congress tightened regulation of new drugs. New drug applications began taking longer, putting off the start of the payoffs from research. The regulations also made research more expensive, by adding requirements, and shortened the whole income stream by taking up time, cutting into the period of patent-protected high profits. The rate of return to research fell. By the above reasoning, that should cause less to be spent on research, so fewer new drugs would be developed.

There are two problems with this argument. One is that drug industry research spending has increased since 1962, even allowing for inflation. The rate of return is evidently still good enough to attract money into research.

The second problem is that regulation is there for a purpose: to keep unsafe and ineffective drugs off of the market. The industry's record is not spotless. "Research" is not necessarily good, unless it's research that might lead to safe and effective products.

Any testing system, whether adopted voluntarily by industry or imposed by government, discourages investment. The price you pay for safety and effectiveness assurance is a reduction in innovation. How much assurance do we get? Is the price too high?

These are issues that are better handled in class discussion than on a computer. I hope that you now understand what the internal rate of return is and how the concept figures in the controversy.
 
 

Internal Rate of Return -- Review and Summary

An income stream for an investment is all of the investment's costs and payoffs, along with when each cost and payoff will happen.

The present value of an investment is the amount of money you'd need now to be able to duplicate the investment's income stream. The present value is calculated using a discount rate which you set to equal your bank's interest rate or the rate of return of some other alternative investment.

The internal rate of return is the discount rate that makes the present value of the investment's costs and payoffs add up to 0.

From the applications:

The yield to maturity of a discounted bond equals its internal rate of return.

Investments with higher internal rates of return attract money away from investments with lower internal rates of return.

If a kind of investment has a persistently high internal rate of return, something is preventing the market from reaching a competitive equilibrium.

Regulation can reduce the rate of return to innovation, just by delaying the payoffs. How to protect the public without stifling innovation is a major problem of regulation, in pharmaceuticals, for example.
 

Perils of Using the Internal Rate of Return

The internal rate of return is not a good way evaluate an investment that has costs later rather than just earlier.  An example of that would be an investment that generates an environmental problem that will require a cleanup at the end of the income stream.  For some such investments, the worse investments have higher internal rates of return.  Please see the next tutorial.

That's all for now. Thanks for participating! 

Comments? Please e-mail me at
To the list of tutorials